Frog Fractions 2 Writeup
Boston Key Party CTF 2016

Turns out Frog Fractions 2 is not battletoads.

When you run this challenge, it gets input and prints: Nope! You need to practice your fractions! To find the logic for final input checking, I used IDA to search for cross references to the failed output. Weirdly, the binary has no strings pertaining to success or failure. Still, we need to find a way to print some way to print something else.

Throughout the binary, we see references to GMP functions. GMP is an arbitrary precision arithmetic library with bindings for many languages. We’re probably dealing with big numbers…

At the beginning of the program, there are several calls to __gmpz_init. The “z” refers to the mathematical notation for the set of all integers. gmpz_init takes one argument, an mpz_t, which is actually a pointer to a special struct as evidenced by the lea instruction, and returns a new mpz_t. The __gmpz_set_ui function sets an mpz_t to an unsigned integer. Below, we see two integers initialized with one, int1, set to 1019.

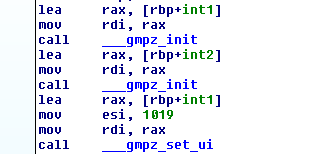
GMP integer initialization

After initializing these two integers, the program creates a number by raising each prime to the power of the ASCII value of corresponding input characters and multiplying it with int1. For instance, if the input is AB the first prime, 2, is raised to 0x41 and the second prime, 3, is raised to 0x42. Thus, the resulting number is 1019 * 2^0x41 * 3^0x42.

__gmpz_pow_ui takes three arguments: an mpz_t to store the value, an mpz_t to be the base, and an unsiged int for the exponent. __gmpz_mul has a similar signature: an mpz_t to store the value and 2 operands of type mpz_t.

Generate number from primes

The following pseudocode is equivalent:

n = 1019
for i, c in enumerate(input):
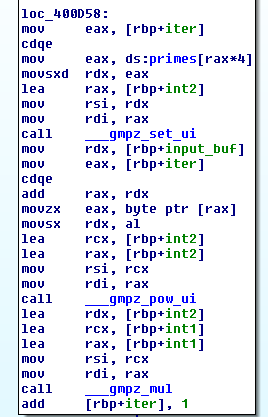
	n *= primes[i] ** ord(c)

Following the creation of int1, the program reads in a series of numerical pairs, which I called x’s and y’s, from program. __gmp_sscanf functions the same as sscanf taking a string pointer, a format string, and pointers to store the scanned values.

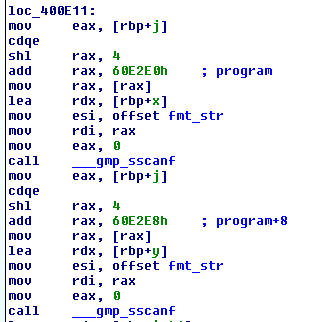
Load numbers from program

Number strings in program (there’s ~250 pairs total):

Program number strings

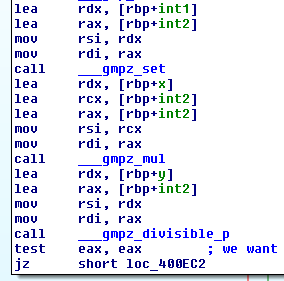
Next, the program checks that each x/y pair satisfies the relationship that x * int1 is evenly divisible by y. If it doesn’t, bad things happen and the program output remains the same.

__gmpz_set sets the first mpz_t equal to the second. __gmpz_mul multiplies the last two mpz_t’s and stores the result in the first. Finally, __gmpz_divisible_p checks if the second mpz_t evenly divides the first.

Test for divisibility

To create a number that satisfies this relationship, I initially tried messing around with iteratively setting n to the lcm of y and x * n and dividing the result by x to cancel out its factors. Unfortunately, this number didn’t work and printed out the same message.

I realized that if I represent each number as a mapping of its factors to their corresponding exponent, I can simplify the process. This time, I iteratively set n using the following expression:

n = n | (y - (x | n))

Note that the OR, AND, and subtraction signs stand for set operations in python. Since I am using a multiset (Counter in python) to represent the mapping, these operations differ slightly from normal set operations. The OR, or union, operation creates a new set with the values from both sets; if there are two instances of the same factor, it keeps the greater exponent. Likewise, the AND, or intersection, operation creates a new set with only factors that show up in both; if there are two instances of the same factor, it keeps the smaller exponent. The subtraction operation sets each exponent equal to exponent(left) - exponent(right).

Examining the above expression, x & n is equivalent to asking what factors do x and n together have. Then y - (x | n) asks what factors does y have that x and n do not share, or what factors does n need to make itself times x divisible by y. Finally, we add those factors to n with n | (y - (x | n)).

Now that we have a prime factorization of the number needed to solve the challenge, we just need to write it to the challenge input format. Recall that the program generated an input number by raising each prime to the ASCII value of the corresponding input. The following code generates the input from the multiset we used to represent n:

s = ""
for p, e in sorted(n.items):
	s += chr(e)

The resulting string is: KEY{(By the way, this challenge would be much easier with a cybernetic frog brain)} – a.k.a. the flag.

Helpful references:

*****
Written by on